Tackling Long-Tailed Category Distribution

Under Domain Shifts

Abstract

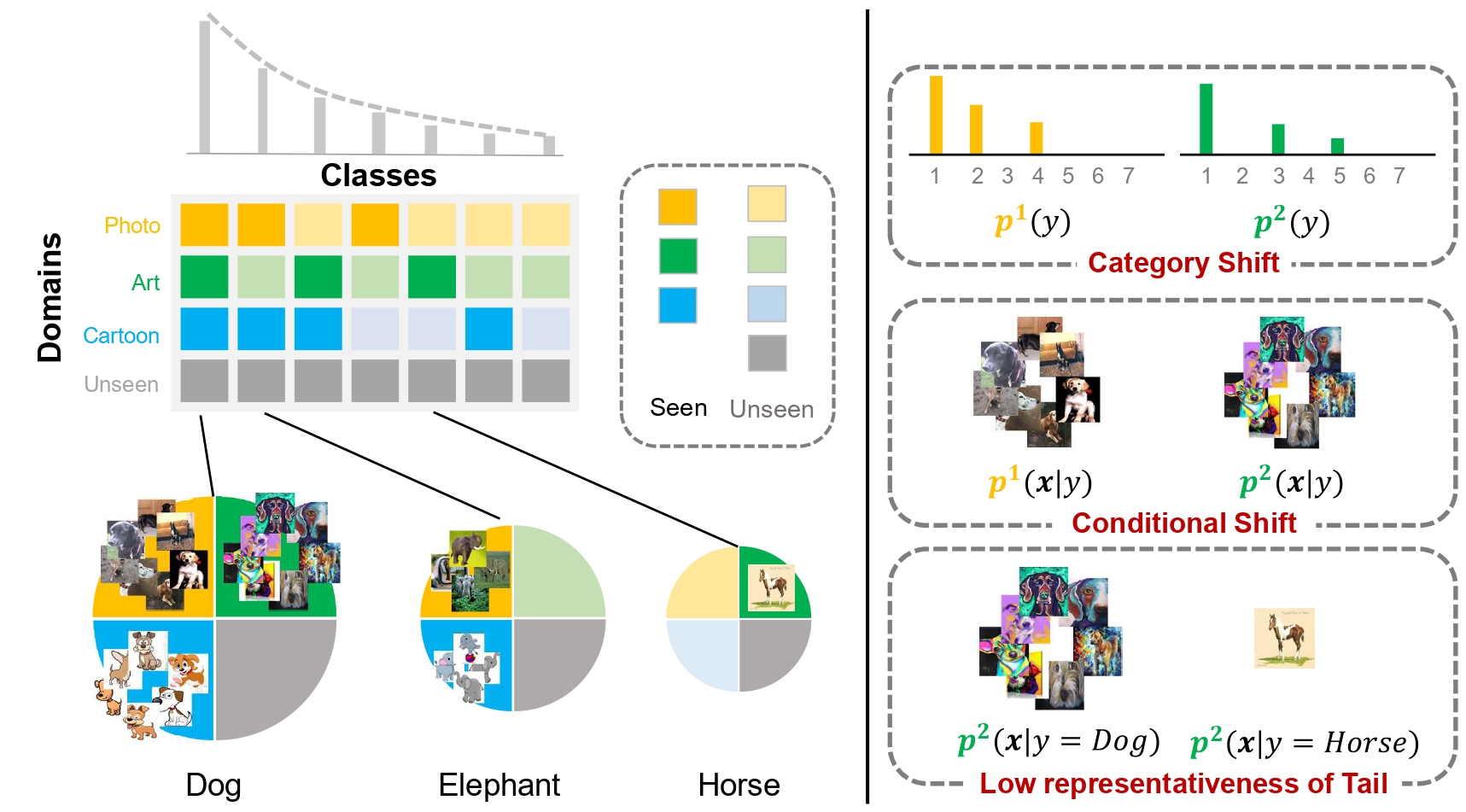
Machine learning models fail to perform well on real-world applications when 1) the category distribution P(Y) of the training dataset suffers from long-tailed distribution and 2) the test data is drawn from different conditional distributions P(X|Y). Existing approaches cannot handle the scenario where both issues exist, which however is common for real-world applications. In this study, we took a step forward and looked into the problem of long-tailed classification under domain shifts. By taking both the categorical distribution bias and conditional distribution shifts into account, we designed three novel core functional blocks including Distribution Calibrated Classification Loss, Visual-Semantic Mapping and Semantic-Similarity Guided Augmentation. Furthermore, we adopted a meta-learning framework which integrates the three blocks to improve domain generalization on unseen target domains. Two new datasets were proposed for long-tailed classification under domain shifts, named AWA2-LTS and ImageNet-LTS. We evaluated our method on the two datasets and extensive experimental results demonstrate that our proposed method can achieve superior performance over state-of-the-art long-tailed/domain generalization approaches and the combinations.

Highlights

We summarized four main issues in Long-Tailed Category Distribution under Domain Shifts (LT-DS). The empricial loss on a testing domain can be formulated as below,

\[ \epsilon = \mathbb{E}_{\color{blue}{m\sim {P_{\mathcal{D}_{te}}}}} \mathbb{E}_{(\mathbf{x},y)\sim \color{blue}{p^m(\boldsymbol{x},y)}} \mathcal{L}(h\circ f(\boldsymbol{x}), y) \] \[ = \mathbb{E}_{{\color{blue}{m\sim {P_{\mathcal{D}_{te}}}}}\\ \color{red}{n\sim P_{{\mathcal{D}_{tr}}}}} \mathbb{E}_{(\boldsymbol{x},y)\sim \color{red}{p^n(\boldsymbol{x},y)}} \mathcal{L}(h\circ f(\boldsymbol{x}), y) \frac{p^\color{blue}{m}(f(\boldsymbol{x}),y)}{p^\color{red}{n}(f(\boldsymbol{x}),y)} \] \[ = \mathbb{E}_{\color{blue}{m\sim {P_{\color{blue}{\mathcal{D}_{te}}}}}\\ \color{red}{n\sim P_{\color{red}{\mathcal{D}_{tr}}}}} \mathbb{E}_{(\boldsymbol{x},y)\sim \color{red}{p^n(\boldsymbol{x},y)}} \mathcal{L}(h\circ f(\boldsymbol{x}), y) \frac{p^\color{blue}{m}(y)p^\color{blue}{m}(f(\boldsymbol{x})|y)}{p^\color{red}{n}(y)p^\color{red}{n}(f(\boldsymbol{x})|y)} \]

Category Shifts - \(p(y)\)




✔

Distribution Calibrated Classification Loss - Model \(\frac{p^{m}(y)}{p^{n}(y)}\) across domains
\[ -\log\frac{n_{y_i}^{d_i} \exp{([h\circ f(\boldsymbol{x}_i)]_{y_i}})}{\sum_{c=1}^C n_c^{d_i} \exp({[h\circ f(\boldsymbol{x}_i)]_{c})}}\]

Conditional Shifts - \(p(f(\boldsymbol{x})|y)\)




✔

Visual-Semantic Mapping - Align \(p(f(\boldsymbol{x})|y)\) across domains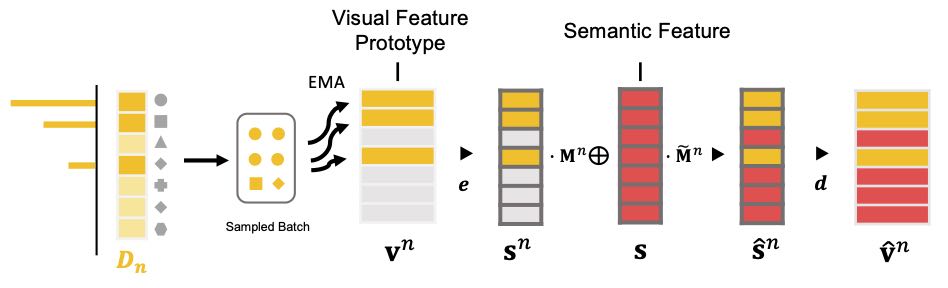




Transformation between domain-specific visual prototype and semantic embeddings.


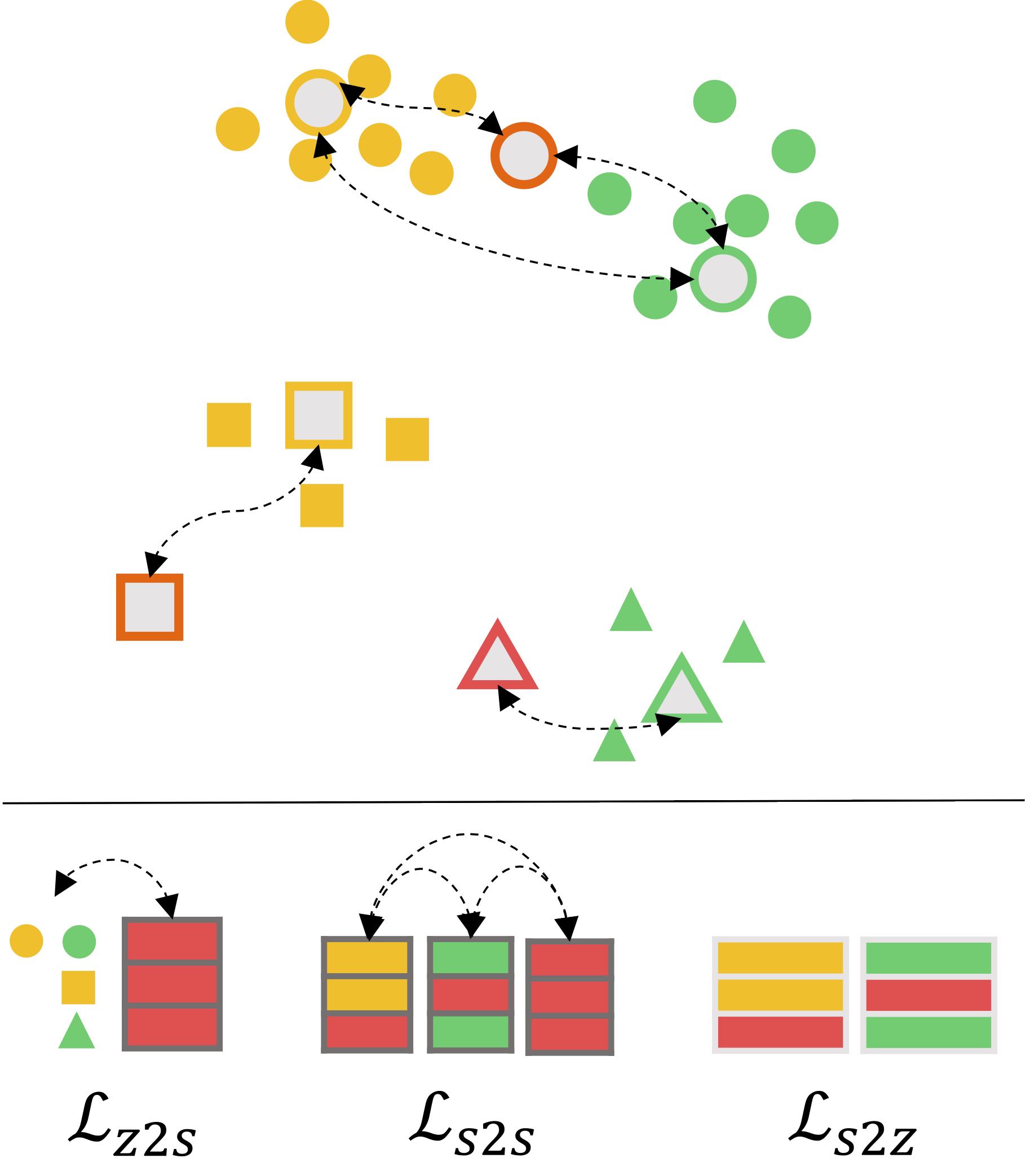
Illustration of visual-semantic mapping.



Low-Representativeness of Tail Classes - \(p(f(\boldsymbol{x})|y=tail)\)




✔

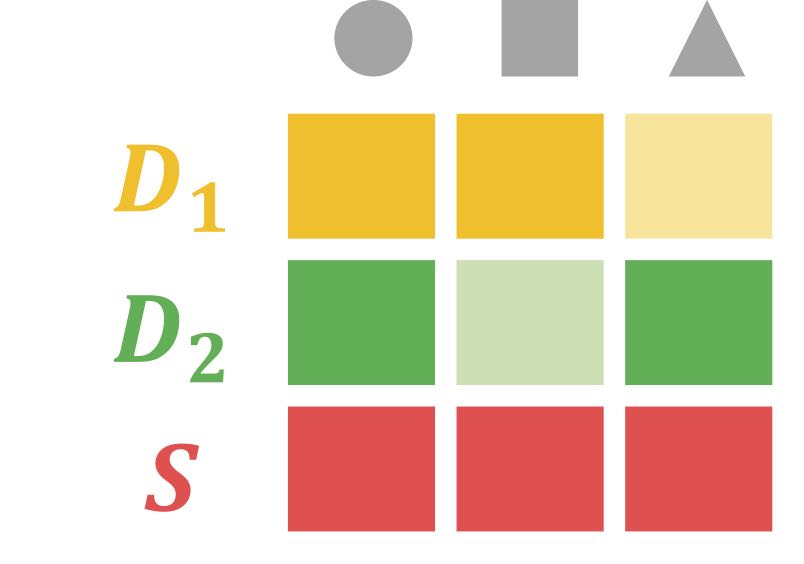
Semantic-Similarity Guided Augmentation - Model \(p(f(\mathbf{x})|y)\)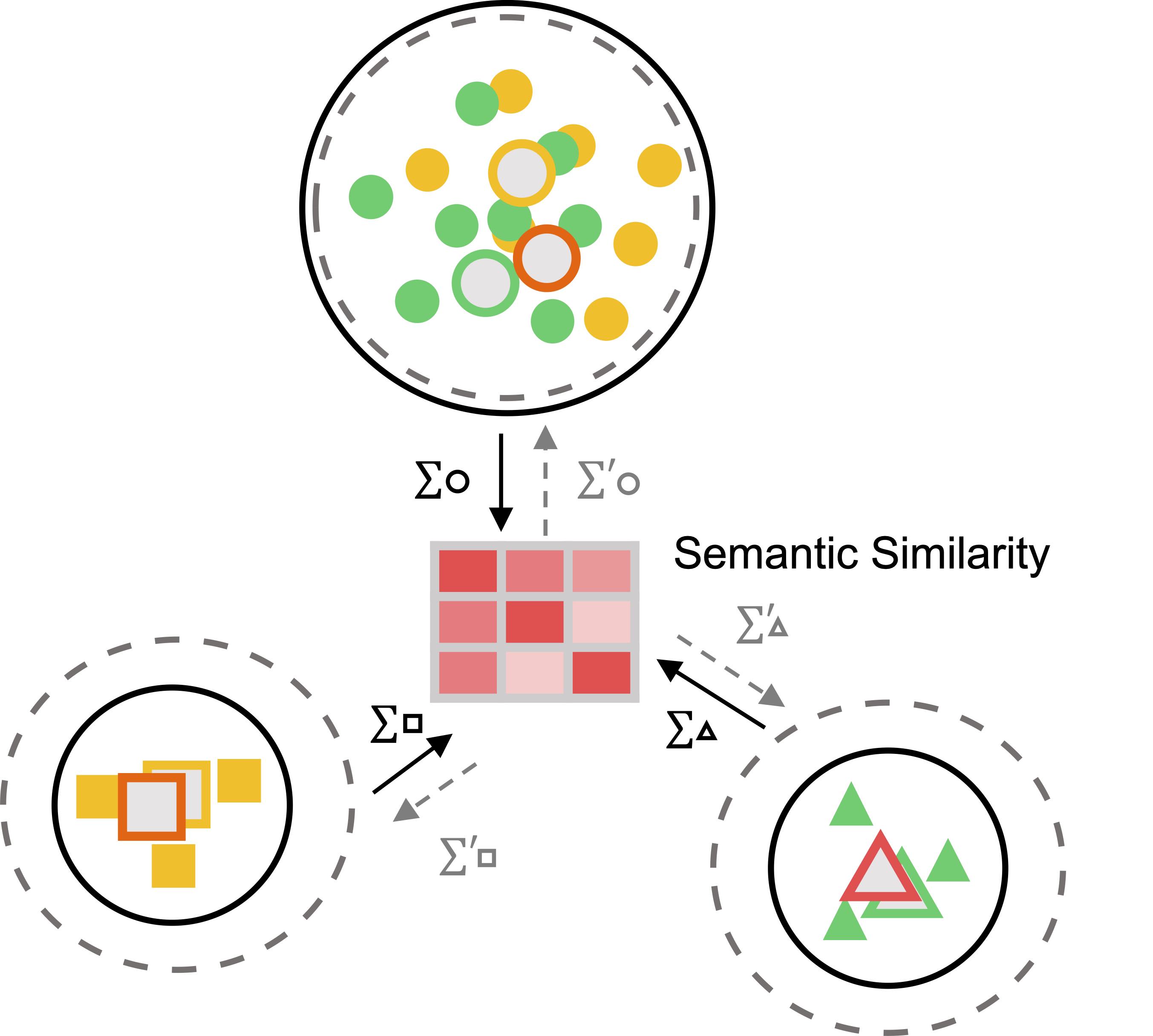



Illustration of semantic-similarity guided augmentation to facilitate distribution modelling, especially tail classes.
\[ Sim_c = \{\mathbf{s}_c^T\mathbf{s}_i|i=1,2,\&...,C\} ; \] \[\mathbf{k}_c = \{i | \mathbf{s}_c^T\mathbf{s}_i \in topk(Sim_c)\},\] \[\mathbf{\Sigma}'_c = \frac{\sum_{k\in \mathbf{k}_c}{n_k}\mathbf{\Sigma}_k}{\sum_{k\in \mathbf{k}_c} n_k}. \]

Generalization of \(f(\boldsymbol{x})\)




✔

Meta-Learning Framework- Handle data from novel domains

Datasets

We simulated two LT-DS datasets for benchmarking, AWA2-LTS and ImageNet-LTS, on top of the established AWA2 and ImageNet-LT datasets. We provide detailed instructions on dataset curation.

Visualization of different styles.

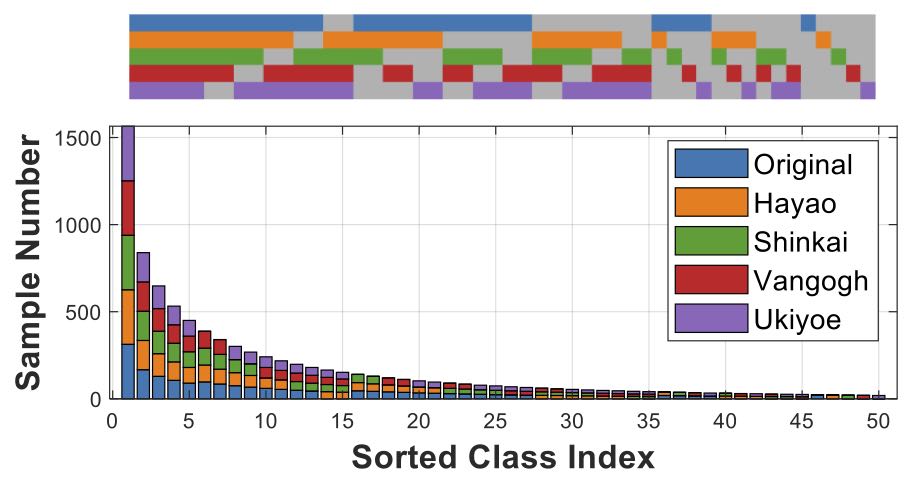
AWA2-LTS

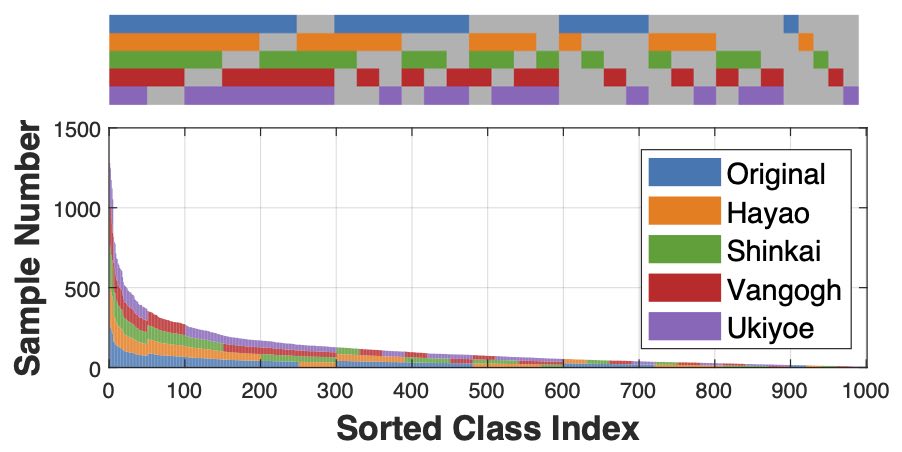
ImageNet-LTS

Citation

@inproceedings{gu2022tackling,
  title={Tackling Long-Tailed Category Distribution Under Domain Shifts},
  author={Gu, Xiao and Guo, Yao and Li, Zeju and Qiu, Jianing and Dou, Qi and Liu, Yuxuan and Lo, Benny and Yang, Guang-Zhong},
  booktitle={ECCV},
  year={2022}
}